66. Силы, сходящиеся в одной точке и лежащие в одной плоскости
Многоугольник сил
Если линии действия сил, приложенных к твердому телу, пересекаются в одной точке, то такие силы называются сходящимися (рис. 40, a).
Сходящиеся силы — это силы, линии действия которых пересекаются в одной точке. Это означает, что все силы действуют через одну общую точку, что упрощает анализ их взаимодействия и позволяет использовать методы векторного сложения для нахождения равнодействующей силы.
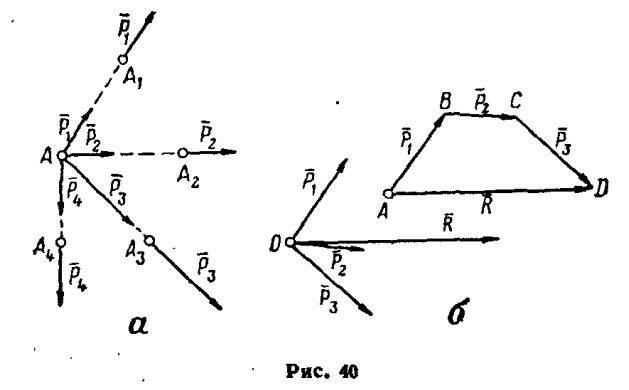
Равнодействующая сходящихся сил равна замыкающей стороне многоугольника сил, построенного на слагаемых силах (рис. 40, б):
\[
\vec{R} = \vec{P_1} + \vec{P_2} + \ldots + \vec{P_n} = \vec{AD}
\]
Аналитический способ нахождения равнодействующей силы
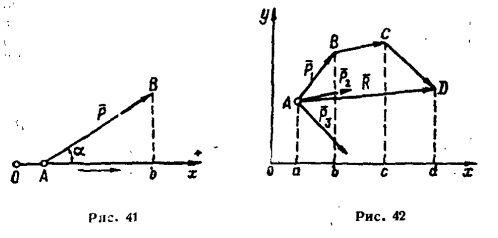
Проекция силы на ось равна произведению величины силы на косинус угла между силой и положительным направлением оси (рис. 41):
\[
P_x = P \cos \alpha
\]
где \( P_x = Ab \) — проекция силы \( P \) на ось \( x \).
Проекция равнодействующей на какую-нибудь ось равна алгебраической сумме проекций слагаемых сил на ту же ось (рис. 42):
\(R_x = P_{1x} + P_{2x} + \ldots + P_{nx} \) или короче: \(R_x = \sum P_x\)
Аналогично для проекций на ось \( y \):
\(R_y = P_{1y} + P_{2y} + \ldots + P_{ny}\) или: \(R_y = \sum P_y\)
Величина равнодействующей по её проекциям определяется по формуле:
\[
R = \sqrt{R_x^2 + R_y^2}
\]
Эти формулы позволяют найти величину и направление равнодействующей силы, зная проекции слагаемых сил на координатные оси.
Условие равновесия сил, сходящихся в одной точке и лежащих в одной плоскости
Для равновесия сил, сходящихся в одной точке и лежащих в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из двух координатных осей равнялась нулю. Это можно выразить следующими уравнениями:
\[
\sum P_{ix} = 0
\]
\[
\sum P_{iy} = 0
\]
где:
- \(\sum P_{ix}\) — алгебраическая сумма проекций всех сил на ось \(x\);
- \(\sum P_{iy}\) — алгебраическая сумма проекций всех сил на ось \(y\).
- Механика Справочник авиатехника
- Вторник, 03 июня 2025
