64-65. Треугольник сил. Действие и равнодействие. Реакция связей.
Равнодействующая двух сил, приложенных в одной точке и направленных под углом друг к другу, приложена в той же точке и изображается диагональю параллелограмма, построенного на данных силах как на сторонах (рис. 39):
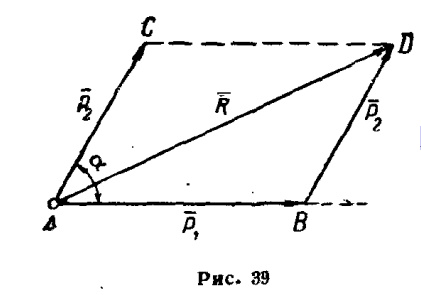
\[ \vec{R} = \vec{P_1} + \vec{P_2} \]
Величина равнодействующей \( R \) определяется по формуле:
\[ R = \sqrt{P_1^2 + P_2^2 + 2P_1P_2 \cos \alpha} \]
где:
- \( \vec{P_1} \) и \( \vec{P_2} \) — векторы двух сил;
- \( P_1 \) и \( P_2 \) — величины этих сил;
- \( \alpha \) — угол между направлениями этих сил.
Эта формула позволяет найти величину равнодействующей силы, зная величины и направления двух исходных сил.
Свободное и несвободное тело
Тело называется свободным, если оно может получить любое перемещение в пространстве. Примерами свободных тел являются самолет и воздушный шар в полете.
Если же перемещение тела в пространстве ограничено, то такое тело называется несвободным.
Связи и реакции связей
Тела, стесняющие движение данного тела, называются связями. Сила, с которой связь действует на данное тело, называется реакцией связи или просто реакцией.
На основании третьего закона Ньютона реакции связей равны по величине и направлены противоположно силам, с которыми тело действует на связи.
Это означает:
... если тело оказывает давление на связь, то связь оказывает равное и противоположно направленное давление на тело.
- Механика Справочник авиатехника
- Вторник, 03 июня 2025
