54. Колебательный контур
Колебательный контур (идеальный) — это цепь, состоящая из индуктивности \( L \) и емкости \( C \). В реальных условиях все контуры обладают активным сопротивлением \( R \), которое характеризует потери энергии в контуре.
Параметры контура
Параметры контура \( L \), \( C \) и \( R \) определяют соотношение между напряжением и током в цепи, частоту колебаний \( f \) и добротность контура \( Q \). Определенным параметрам контура соответствует только одна частота, на которой наступает явление резонанса, называемое резонансной частотой \( f_0 \).
Резонанс
Резонанс — это явление в колебательном контуре, при котором амплитуда колебаний принимает максимальное значение. Резонансная частота \( f_0 \) определяется формулой:
\[
f_0 = \frac{1}{2\pi \sqrt{LC}}
\]
где:
- \( f_0 \) — резонансная частота,
- \( L \) — индуктивность, Гн,
- \( C \) — емкость, Ф,
- \( R \) — сопротивление, Ом,
- \( \pi \approx 3.14 \).
Добротность контура
Добротность контура \( Q \) определяется как отношение индуктивного сопротивления \( X_L \) к активному сопротивлению \( R \):
\[
Q = \frac{X_L}{R} = \frac{2\pi f_0 L}{R} = \frac{\omega L}{R}
\]
где:
- \( X_L = \omega L \) — индуктивное сопротивление,
- \( R \) — активное сопротивление,
- \( \omega = 2\pi f \) — угловая частота.
Схема последовательного RLC-контура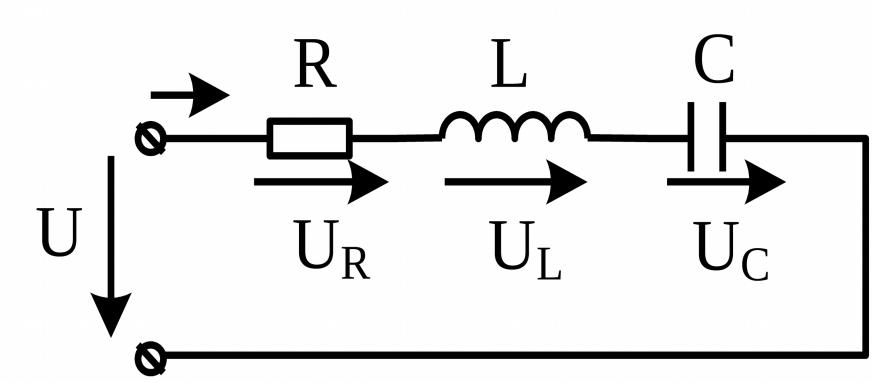 
(Здесь:
- \( R \) — резистор (активное сопротивление),
- \( L \) — катушка индуктивности,
- \( C \) — конденсатор.)
График зависимости добротности от частоты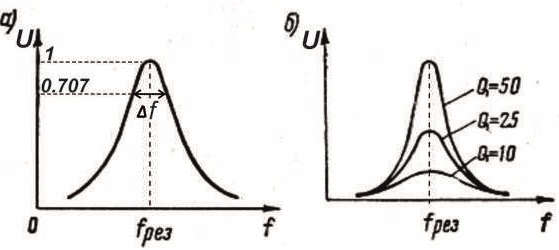 
\( f_{рез} \) — резонансная частота
\( U \) — напряжение в колебательном контуре
Чем выше \( Q \), тем острее резонансный пик
\( Q_{50} > Q_{25} > Q_{10} \) — примеры разных добротностей.
Формула определения добротности также имеет вид: Q = f рез/Δf
Катушки индуктивности
Катушки индуктивности характеризуются величиной индуктивности \( L \) и добротностью \( Q \). Добротность катушки тем выше, чем больше отношение ее индуктивного сопротивления \( X_L \) к активному сопротивлению \( R \) потерь в катушке:
\[
Q = \frac{2\pi f L}{R}
\]
Для получения малогабаритных катушек с высокой добротностью применяются магнитные сердечники. Магнитные сердечники, кроме того, можно изменять (для настройки) индуктивность катушки. Магнитные сердечники характеризуются действующей магнитной проницаемостью \( \mu \), представляющей собой отношение индуктивности какой-либо катушки с сердечником к индуктивности той же катушки без сердечника.
На высоких радиочастотах для магнитных сердечников применяются материалы с малыми потерями — магнетит, альсифер, ферриты.
Дроссель высокой частоты
Дроссель высокой частоты — это индуктивность, включаемая в цепь для преграждения пути токам высокой частоты. Она имеет большую индуктивность и малую емкость, т.е. большое сопротивление для токов высокой частоты. Для токов низкой частоты применяются дроссели с железными сердечниками.
- 63